hexadecimal
What is hexadecimal?
Hexadecimal is a numbering system with base 16. It can be used to represent large numbers with fewer digits.
In this system there are 16 symbols or possible digit values from 0 to 9, followed by six alphabetic characters -- A, B, C, D, E and F. These characters are used to represent decimal values from 10 to 15 in single bits.
Hexadecimal explained
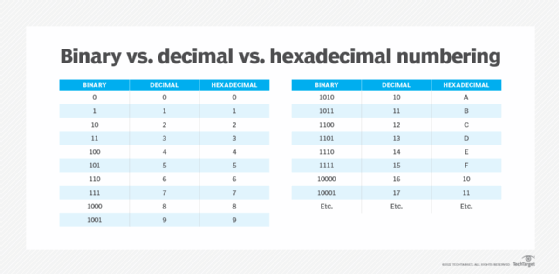
Hexadecimal -- also known as Base 16 or hex -- is one of four numbering systems. The other three are decimal (base 10), binary (base 2) and octal (base 8).
Here's what the decimal and hexadecimal systems look like for digits 0 to 15.
| Decimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| Hexadecimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
The hexadecimal system contains 16 sequential numbers as base units, including 0. The first nine numbers (0 to 9) are the same ones commonly used in the decimal system. The next six two-digit numbers (10 to 15) are represented by the letters A through F. This is how the hex system uses the numbers from 0 to 9 and the capital letters A to F to represent the equivalent decimal number.
In this numbering system, each digit's position is 16 times more significant than the digit in the previous position. The hex number starts with the least significant digit on the right-hand side. The numeric value of this number is calculated by multiplying each digit by the value of its position and then adding the products. This is why hexadecimal is a positional or weighted number system.
The need for hexadecimal numbers
In computing systems, the binary string equivalents of large decimal numbers can become quite long. When 16- or 32-bit numbers are involved, it becomes difficult to read and write them without producing errors. These problems can be overcome by arranging the binary numbers into groups of four bits, i.e., by using the hexadecimal numbering system.
The format of hex numbers is more compact than binary numbers because they can represent large binary numbers with fewer digits. As a result, they are easier to understand than long binary strings of 1s and 0s.
Representation of hexadecimal numbers
In hex, four digits of a binary number can be represented by a single hex digit. Dividing a binary number into 4-bit sets means that each set can have a possible value of between 0000 and 1111, allowing 16 number combinations from 0 to 15. With the base value as 16, the maximum value of a digit is 15.
It's easy to convert a binary number into a hexadecimal number and vice versa. Here's how these numbers are represented in each system:
| Hexadecimal number |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 4-bit binary number |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
| Hexadecimal number |
8 |
9 |
A |
B |
C |
D |
E |
F |
| 4-bit binary number |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
Additionally, the digits to the left of hexadecimal point have weights 160, 161, 162 and so on. Similarly, the positions to the right have weights of 16-1, 16-2, etc.
Example
To represent the decimal number 512 in hex:
Decimal value = 512
512 = 2x162+0x161+0x160=200
Hex value = 200
Converting binary and decimal numbers to hexadecimal
- Converting binary to hexadecimal
To convert binary numbers to hexadecimal, four binary digits must be mapped or converted to one hexadecimal digit. Here's how the conversion works:
- Split the binary value into groups of four, starting from the digit at the far right.
- Match each group of four against the corresponding hexadecimal value.
- Represent the original binary number in hexadecimal format.
Example
Here's how to convert the binary number 1011010101100001 to hex form:
Step 1: Split the binary value into groups of four.
| 1011 |
0101 |
0110 |
0001 |
Step 2: Replace each set with a hexadecimal value.
| 1011 |
0101 |
0110 |
0001 |
| B |
5 |
6 |
1 |
Step 3: Represent binary as hex
10110101011000012 = B56116
- Converting decimal to hexadecimal
The process of converting a decimal number to hexadecimal is simple, although there are more steps:
- Divide the decimal number by 16.
- Write the remainder in hexadecimal form.
- Divide the result by 16.
- Repeat steps 2 and 3 until the result is 0.
The hexadecimal value obtained is the sequence of remainders from the last to the first.
Example
Here's how to convert the decimal number 1128 to hexadecimal:
Step 1: Divide 1128 by 16 to arrive at the result of 70 and remainder 8.
Step 2: Divide the result (70) by 16 to get a new result 4 and remainder 6.
Step 3: Divide the result (4) by 16 to get the result of 0 and remainder 4.
Step 4: Represent the hexadecimal number as the sequence of remainders from the last to the first.
112810 = 46816
Hexadecimal identifiers
Hexadecimal numbers are usually prefixed or suffixed with identifiers to avoid confusion during reading or writing and to make it easy to distinguish hex numbers from decimal numbers. Some common hex identifiers include:
| Identifier | Usage | Example |
| % |
Commonly used in URLs to specify characters like spaces |
%2 |
| # |
Used in HTML language as color references |
#RR5687 |
| 0h |
Used in programmable graphic calculators |
0h7D |
| \x |
Used in HTML, XML and other languages to express character control codes |
\x08: Backspace \x1B: Escape |
| 0x |
Used in UNIX and C-based programming |
0x54EF |
Other identifiers are also available; however, they are usually limited to specific programming languages and cannot be used interchangeably with other languages.
Hexadecimal applications
The hexadecimal numerical system is particularly useful in computer programming and microprocessors. Developers use it to describe colors on webpages, describe memory locations for each byte, to specify certain characters and more. Hex numbers are also used in microcontrollers to simplify data handling and manipulation. Other possible applications are data science and analytics, machine learning and artificial intelligence.
Hexadecimal advantages and disadvantages
Hex numbers are compact and use less memory, so more numbers can be stored in computer systems. Their small size also makes input-output handling easier compared to other numbering formats. Because it's easy to convert hexadecimal to binary and vice versa, the system is widely used in computer programming. It is also useful to represent computer memory addresses.
One drawback of the hexadecimal system is that it can be difficult to perform complex mathematical operations like multiplication and division. Hex numbers are also difficult to read and write compared to decimal numbers.
See also: Shared Key Authentication, Blowfish, network packet, big-endian and little-endian, globally unique identifier, universally unique identifier
