Mathematical symbols
This list of commonly used mathematical symbols explains what each math symbol is, how it is used and provides a sample expression.
| Symbol | What it is | How it is read | How it is used | Sample expression |
| + | Addition sign Logical OR symbol |
... plus ... ... or ... |
Sum of a few values Logical disjunction |
3 + 5 = 8 ¬(A + B) = ¬A * ¬B |
| * | Multiplication sign Logical AND symbol |
... times ... ... and ... |
Product of two values Logical conjunction |
3 x 5 = 15 ¬(A * B) = ¬A + ¬B |
| x | Multiplication sign | ... times ... | Product of two values | 3 x 5 = 15 |
| · | Multiplication sign | ... times ... | Product of two values | 3 · 5 = 15 |
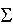 |
summation sign | The summation of ... | Sum of many or infinitely many values |
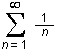 |
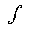 |
Integral sign | The integral of ... | integration | 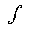 x2 dx = x3/3 + c x2 dx = x3/3 + c |
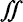 |
Double integral sign | The double integral of ... | integration | 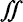 f(x,y) dx dy f(x,y) dx dy |
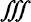 |
Triple integral sign | The triple integral of ... | integration | 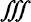 f(x,y,z) dx dy dz f(x,y,z) dx dy dz |
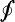 |
Line integral sign | The line integral of ... | integration | 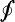 F F  dx dx |
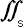 |
Surface integral sign | The surface integral of ... | integration | 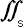 F(x,y,z) dx dy F(x,y,z) dx dy |
| - | Subtraction sign Minus sign |
... minus ... Negative... |
Difference of two values, negative number |
3 - 5 = -2 |
| ± | Plus/minus sign | ... plus or minus ... | Expression of range, error, or tolerance |
500 kbps ± 10% |
 |
dot product sign | ... dot ... | Scalar (dot) product of two vectors |
A  B = B B = B  A A |
| x | Cross product sign | ... cross ... | Vector (cross) product of two vectors |
A x B = - (B x A) |
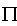 |
Product sign | The product of ... | Product of three up to infinitely many values |
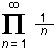 |
| ^ | Carat | ... to the power of ... | exponent | 2 ^ 5 = 32 |
| ! | Exclamation | ... factorial | Product of all positive integers up to a certain value |
5! = 120 |
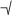 |
Surd | ... root of ... | Algebraic expressions | z = 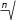 (x + y) (x + y) |
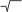 |
Square root symbol | The square root of ... | Algebraic expressions | 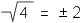 |
| ... | Continuation sign | ... and so on up to ... ... and so on indefinitely |
Extension of sequence | S = {1, 2, 3, ...} |
| / | Slash | ... divided by ... ... over ... |
Division | 3/4 = 0.75 |
| ÷ | Division sign | ... divided by ... | Division | 3 ÷ 4 = 0.75 |
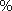 |
Percent symbol | ... percent ... | Proportion | 0.032 = 3.2 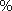 |
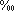 |
Per mil symbol | ... per mil ... | Proportion | 0.032 = 32 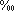 |
| : | Colon, ratio sign |
... is to ... ... such that ... ... it is true that ... |
Division or ratio, symbol following logical quantifier or used in defining a set |
2:4 = 20:40
S = {x : x < 3} |
| | | Vertical line | ... such that ... ...it is true that ... |
Symbol following logical quantifier or used in defining a set |
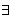 x | x > 4 and x < 5 x | x > 4 and x < 5
S = {x | x < 3} |
| :: | Double colon | ... averaged with ... | arithmetic mean | 3 :: 11 = 7 |
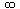 |
lemniscate | ... infinity ... increases without limit |
Infinite summations Infinite sequence Limit |
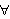 x : x < x : x < 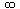 |
| ( ) | Parentheses | ...quantity... ...list... ...set of coordinates... ...open interval |
Denotes a quantity, list, set of coordinates, or an open interval |
(x + y) + z (a1, a2, a3, a4) (x,y,z) (3,5) |
| [ ] | Square brackets | ... the quantity ... ... the closed interval ... |
Denotes a quantity or a closed interval |
w + [(x + y) + z] [3,5] |
| ( ] | Hybrid brackets | ... the half-open interval ... | Denotes a half-open interval |
(3,5] |
| [ ) | Hybrid brackets | ... the half-open interval ... | Denotes a half-open interval |
[3,5) |
| { } | Curly brackets | ... the quantity ... ... the SET ... |
Denotes a quantity or a SET | E = {2, 4, 6, 8, ...} |
| = | Equal sign | ... equals ... | Indicates two values are the same |
-(-5) = 5 2z2 + 4z - 6 = 0 |
 |
proportionality sign | ... is proportional to ... | Indicates two variables change in direct proportion |
x  y y |
| ~ | Similarity sign | ... is similar to ... | Indicates two objects are geometrically similar |
 ABC ~ ABC ~  DEF DEF |
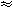 |
Approximate equal sign |
... is approximately equal to ... | Indicates two values are close to each other |
x + y 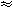 z z |
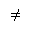 |
Inequality sign | ... is not equal to ... | Indicates two values are different |
x 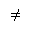 y y |
| < | Inequality sign | ... is less than ... | Indicates value on left is smaller than value on right |
3 < 5 x < y |
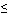 |
Inequality sign | ... is less than or equal to ... ... is at most equal to ... |
Indicates value on left is smaller than or equal to value on right |
x 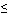 y y |
| > | Inequality sign | ... is greater than ... | Indicates value on left is larger than value on right |
5 > 3 x > y |
| ≥ | Inequality sign | ... is greater than or equal to ... | Indicates value on left is larger than or equal to value on right |
x ≥ y |
| | | | absolute value sign | The absolute value of ... | Distance of value from origin in number line, plane, or space |
| -3 | = 3 |
 |
increment sign, Triangle symbol |
the change in ... triangle ... |
Indicates a small change, Denotes vertices of triangle |
m =  y / y /  x x ABC = ABC =  DEF DEF |
 |
Perpendicularity symbol |
... is perpendicular to ... | Geometry | L  M M |
| // | Parallel symbol | ... is parallel to ... | Geometry | L // M |
 |
Angle symbol | Angle ... | Geometry |  ABC = ABC =  DEF DEF |
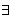 |
Existential quantifier | For some ... There exists a(n) ... |
Logical statements | 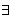 x : x > 4 and x < 5 x : x > 4 and x < 5 |
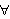 |
Universal quantifier | For all ... For every ... |
Logical statements | 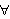 x : x < 0 or x > -1 x : x < 0 or x > -1 |
| ¬ | Logical negation symbol |
not ... | Logical statements | ¬(¬A)  A A |
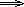 |
logical implication symbol |
... implies ... If ... then ... |
Logical statements | A 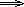 B B |
 |
logical equivalence symbol |
... is logically equivalent to ... ... if and only if .. |
Logical statements | A  B B |
 |
Three dots | ... therefore ... ... it follows that ... |
Logical statements or mathematical proofs |
x = y and y = z x = z x = z |
 |
Element-of symbol |
... is an element of a set ... |
Sets | a  A A |
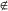 |
Not-element-of symbol |
... is not an element of a set ... |
Sets | b 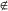 A A |
 |
Subset symbol | ... is a subset of ... | Sets | A  B B |
 |
Proper subset symbol | ... is a proper subset of ... | Sets | A  B B |
 |
Union symbol | ... union ... | Sets | A  B = B B = B  A A |
 |
Intersection symbol | ... intersect ... ... intersected with ... |
Sets | A  B = B B = B  A A |
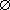 |
Null symbol | The null set The empty set |
Sets | 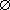 = { } = { } |
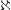 |
Hebrew aleph (uppercase) |
Aleph ... | Transfinite cardinal | 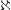 1 + 1 + 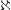 0 = 0 = 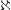 1 1 |
| º | Degree symbol | ... degree(s) | Angular measure Temperature |
T = +20 ºC |
| θ | Greek theta (lowercase) |
... theta ... | Angular variable | θ = 90º |
| φ | Greek phi (lowercase) |
... phi ... | Angular variable |  = 45º = 45º |
| λ | Greek lambda (lowercase) |
... lambda ... | Wavelength Ratio Eigenvalue Lebesgue measure |
 = 70 cm = 70 cm = 3:1 = 3:1 |
| µ | Greek mu (lowercase) |
micro- (10-6) | Prefix multiplier | C = 0.001 µF |
 |
Greek pi (lowercase) |
... pi ... | General science |  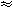 3.14159 3.14159 |
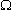 |
Greek omega (uppercase) |
... omega ... | Volume of an object Ohms (resistance) |
R2 = 330 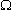 |
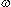 |
Greek omega (lowercase) |
... omega ... | Transfinite ordinal Angular velocity Period |
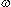 = 36,000 rad/s = 36,000 rad/s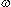 = 1/60 s = 1/60 s |
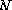 , N , N |
Enhanced or bold N | The set of natural numbers | Number theory Set theory |
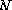 = {0, 1, 2, 3, ...} = {0, 1, 2, 3, ...} |
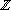 , Z , Z |
Enhanced or bold Z | The set of integers | Number theory Set theory |
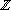 = {0, 1, -1, 2, -2, 3, -3, ...} = {0, 1, -1, 2, -2, 3, -3, ...} |
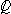 , Q , Q |
Enhanced or bold Q | The set of rational numbers | Number theory Set theory |
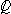 = {a/b | a and b are in = {a/b | a and b are in 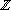 } } |
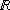 , R , R |
Enhanced or bold R | The set of real numbers | Number theory Set theory |
What is the cardinality of 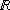 ? ? |







