integer

What is an integer and what are examples of integers?

An integer (pronounced IN-tuh-jer) is a whole number (not a fractional number) that can be positive, negative, or zero.

Examples of integers are: -5, 1, 5, 8, 97, and 3,043.

Examples of numbers that are not integers are: -1.43, 1 3/4, 3.14, .09, and 5,643.1.

The set of integers, denoted Z, is formally defined as follows:

Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}

In mathematical equations, unknown or unspecified integers are represented by lowercase, italicized letters from the "late middle" of the alphabet. The most common are p, q, r, and s.

The set Z is a denumerable set. Denumerability refers to the fact that, even though there might be an infinite number of elements in a set, those elements can be denoted by a list that implies the identity of every element in the set. For example, it is intuitive from the list {..., -3, -2, -1, 0, 1, 2, 3, ...} that 356,804,251 and -67,332 are integers, but 356,804,251.5, -67,332.89, -4/3, and 0.232323 ... are not.

The elements of Z can be paired off one-to-one with the elements of N, the set of natural numbers, with no elements being left out of either set. Let N = {1, 2, 3, ...}. Then the pairing can proceed in this way:

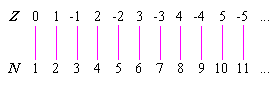
In infinite sets, the existence of a one-to-one correspondence is the litmus test for determining cardinality, or size. The set of natural numbers and the set of rational numbers have the same cardinality as Z. However, the sets of real numbers, imaginary numbers, and complex numbers have cardinality larger than that of Z.